15 Cobb-Douglas Production Function
The first Cobb-Douglas function has been found by Johann Heinrich von Thünen in the first half of the 19th Century, and was completed by the U.S. economist Douglas and Cobb in 1928. It is often used in growth models in different variations. It is usually used in the form
![]() (15.1)
(15.1)
As always the function Y is GDP and K
the capital stock.![]() is generally a
time-variable factor and should increase with time so a technical advance can
be mapped. The exponents a and b add up to 1 in most implementations31, so
is generally a
time-variable factor and should increase with time so a technical advance can
be mapped. The exponents a and b add up to 1 in most implementations31, so![]() and
and![]() holds. Next L
is labor input. So for example, if it is assumed a=0.3 and thus b=0.7,
then one assumes that the share of capital stock is almost 30% and the share of
labor is 70% to the production Y. That's the theory. But again we have
only one equation for calculating the two functions Y and K. We
need but two linearly independent equations32 to find a solution. Next we see
when the factor c(t) is to specify the effect of progress, this effect is
directly related to the free choice of c(t) defined by it self. The
analytical statement can therefore not be truly resilient.
holds. Next L
is labor input. So for example, if it is assumed a=0.3 and thus b=0.7,
then one assumes that the share of capital stock is almost 30% and the share of
labor is 70% to the production Y. That's the theory. But again we have
only one equation for calculating the two functions Y and K. We
need but two linearly independent equations32 to find a solution. Next we see
when the factor c(t) is to specify the effect of progress, this effect is
directly related to the free choice of c(t) defined by it self. The
analytical statement can therefore not be truly resilient.
Furthermore, because the work L is
always a certain proportion d(t) of the GDP Y, we can rearrange
the commonly used function ![]() easily
to
easily
to
![]() (15.2)
(15.2)
which shows that the Cobb-Douglas model again is a special AK-model with
![]() (15.3).
(15.3).
All AK-models have the option to represent by
the choice of ![]() any econometric
model as the desired result. The uncritical acceptance of the CDPF gives such a
requested result, however, some advance: In general one assumes that the input
labor L consists to a specific share of human capital, which results
e.g. from good education, which results in the subformula
any econometric
model as the desired result. The uncritical acceptance of the CDPF gives such a
requested result, however, some advance: In general one assumes that the input
labor L consists to a specific share of human capital, which results
e.g. from good education, which results in the subformula![]() . The CDPF is
then used in order to prove that now education increases the GDP.
. The CDPF is
then used in order to prove that now education increases the GDP.
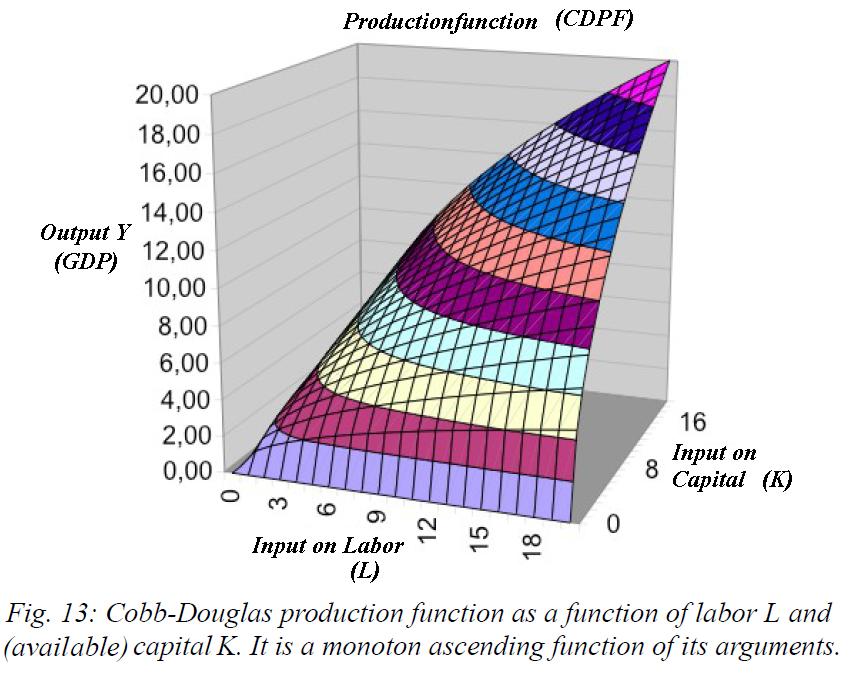
Since the CDPF, as Figure above shows, the function Y will always increase33 for increasing K and L as well, then the answer is clear: The improved human34 capital inevitably increases the GDP.
The deeper cause of such unintended deception lies in the fact that mathematics, and thus any logic, is a science of pure structure. If the structures are mathematically identical, so the calculations are the same. Names and abbreviations, however, are smoke and mirrors and interchangeable. In the modeling thus is always important that the chosen mathematical structure fits as accurately as possible, but at least very close to, the real structure, that means the structure that is connected with the names used.