25 Marginal Utility and Gossen's Law

The marginal utility theory claims the empirically proven relation that

    (25.1)

the marginal utility of a utility functionof the goodsgoes to zero with time .This means that one privately used car produces high value, but the second already relatively less. The third and fourth car can slide into negative value. because of its high costs and only few additional benefits. However, we consider the case of very wealthy consumers well, that there will be purchased six or seven vehicles for private use, such as a number of different sports cars, even though their marginal benefit is actually negative. Empirically, this is explained with the fun factor as one intangible⁵⁰ benefit.

But the cause in the average of the national economy is that the average consumer is not able to buy an additional mobile to create fun, unless he saves it in a different position , so eventually to scrimp and save it. The diminishing marginal utility is explained in the following analysis of this competitive situation of cash flows. This also applies to the example of the affluent consumer. The affluent consumer will not scrimp and save it, but he will substitute it from his investments. As in place of the third sports car he could buy even more from the financial institutions promoted financial products.

Due to the validity of the continuity equation, we are dealing with a total economy that is a substitution economy. From this elementary law can be derived analytically the empirically known laws of marginal utility theory and e.g. also the second law of Gossen and much more. The second law of Gossen states that the amounts of consumer goods of the n goods available to an individual, with the differentiable utility functionand the prices of goods, the second law of Gossen holds:

    (25.2)

For the analytical derivation, we differentiate now the quantity equation for the j-th consumer choice:

(24.3)

But now because of the enormous variety of productsin the last term, this is also given for the term

    (25.3),

because we only have eliminated one but from millions of products, which changes the balance not significantly⁵¹. Then also for all j holds:

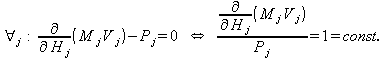    (25.4)

and thus according⁵²

    (25.5)

with the obvious conversion

and     (25.6)

and thus the second law of Gossen resulting directly from the economic equation of continuity. The diminishing marginal utility now is derived from the economic situation of the n-competing products:

    (25.7)

The thus found Gossen utility function says, that the change of use of the n-th productonly then does function, if either the quantity of the i-th product (represented by the amount of moneyavailable for it) with the amendment made bydecreases, or the money has to circulate faster. The latter, however, means that the consumer has to have more money per unit of time, ie a wage⁵³, at his disposal. Without a real general wage increase is therefore:

    (25.8)

what can be change to:

    (25.9)

Has the purchase decision of the n-th product not come due to an improvement in income, then

    (25.10) holds.

The n-th price so decides after the competitive substitution⁵⁴ of the n-th product to the i competing products. We can now look a little closer to this equation, which should indeed result in a diminishing marginal utility. First, we look economically:Interesting there is of course the price, especially the price change. First we assume a lack of improvement in income and with

 

    results          (25.11).

Suppose even that theare all approximately equal⁵⁵ , then we can write for simplicity:

    (25.12)

The marginal benefitis achieved then when

    (25.13)

holds. This means in particular that the price change comes to a standstill as soon as the sum of the changed trading volumes (represented by their monetary equivalent) of the i competing products cancels the change of trade of the n-th product.