44 Spiral Symmetry of Economy

In fact, Y(K) is no parable, but a logarithmic spiral, as we can see in an example here in the slightly lengthened to 260 years⁸⁴ integration.

 

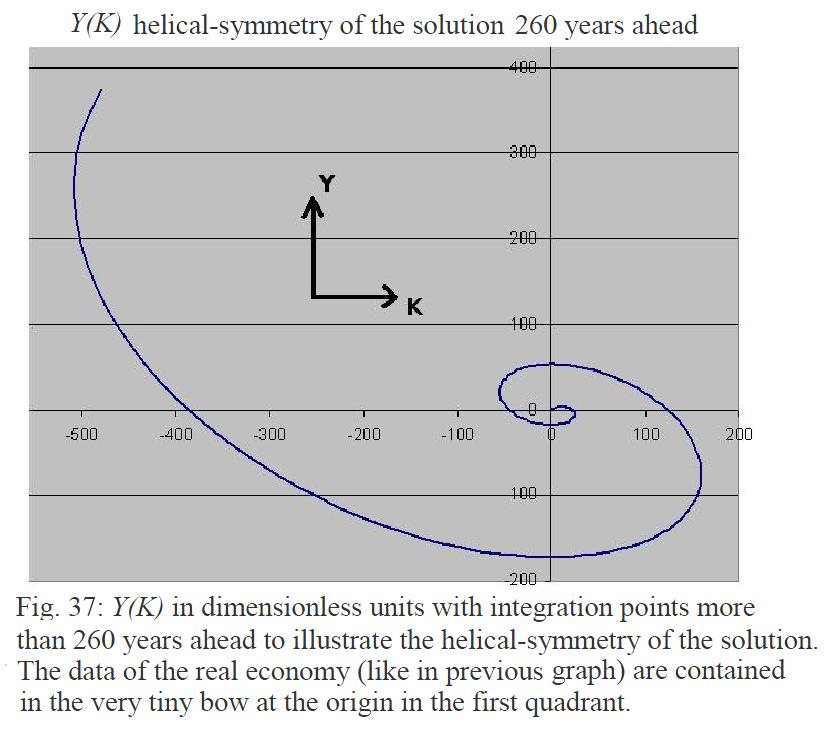
One can change to the logarithm of the axes, thus resulting in the following image by the real part of the beginning of the spiral is in the fourth to the end of the first quadrant.

 

 

Such logarithmic spirals⁸⁵ are subject to certain symmetries.

 

 

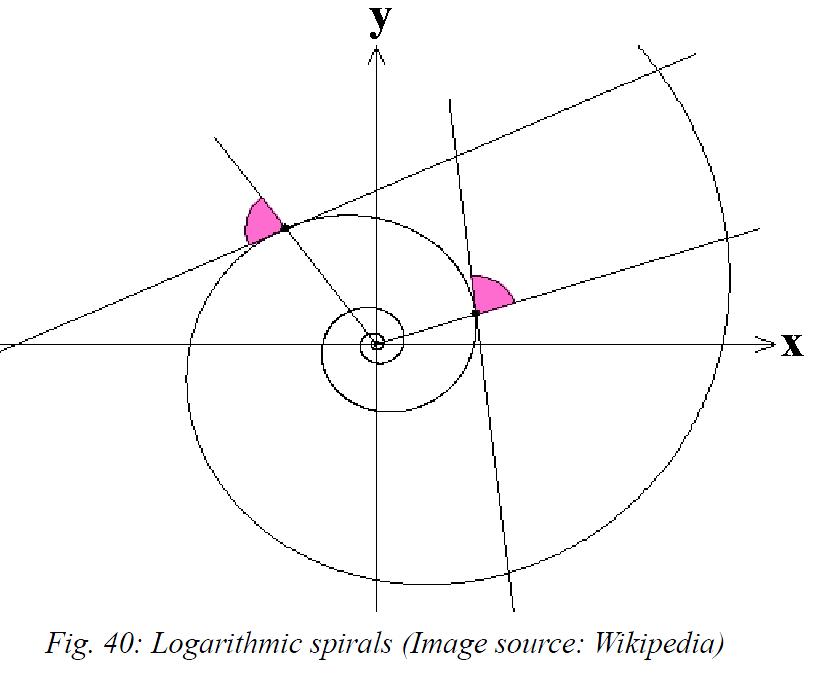
With each rotation, it increases the distance from its center (pole) by the same factor. Each straight line through the pole intersects the spiral at the same angle, for which reason it is also known as equiangular spiral. It can be written in polar coordinates as

    (44.1)

or in Cartesian coordinates as

   (44.2).

Hereis the constant pitch of the spiral with the pitch angle. The name stems from the implicit representation

    (44.3)

whereis the so-called normalized radius.  Elegant the spiral leaves represented in the complex plane:

with     (44.4)

which will prove

    (44.5)

and can finally be written:

    (44.6)

With each turn the radius increases by a constant factor

    (44.7)

The logarithmic spiral is also invariant under a rotation and expansion by the constants. The inversionleads to a reversal of the direction of rotation and mirroring the curve of the y-axis. In the case a = 1, it is only the reflection. For k=0, we obtain the circle as a limiting case of a logarithmic spiral with the equiangular intersection angle of = 90 degrees.