45 Preservation of the Tangent Angle

First, we exploit the symmetry of the constant tangent cutting angle. Our pole vector isand thus the tangent vector is. Thus follows by rule of the scalar-product

    (45.1)

from which follows now the 'economic Pythagoras' :

    (45.2)

Of this we can now solve the Euler-Lagrange equation:

    (45.3)

The results are the three solutions 

    (45.4).

The importance of the first is trivial, it simply states that if no growth takes place through capital investment, then neither capital nor economy⁸⁶ grows. The other solutions can be resolved meaningfully related to the growth rate resulting from capitalization:

    (45.5)

The importance of the real part is that the growth rate with respect to K decreases asdoes. This means that the marginal benefit of capital decreases as with time, a fact which is confirmed by the experience and was treated as part of the special theory already. The amount of the complex vector

    (45.6)

results to the two possible amounts:

    or         (45.7)

The valueis now linked on the quantity equation with the average monetary velocity:

, and thus applies     (45.8).

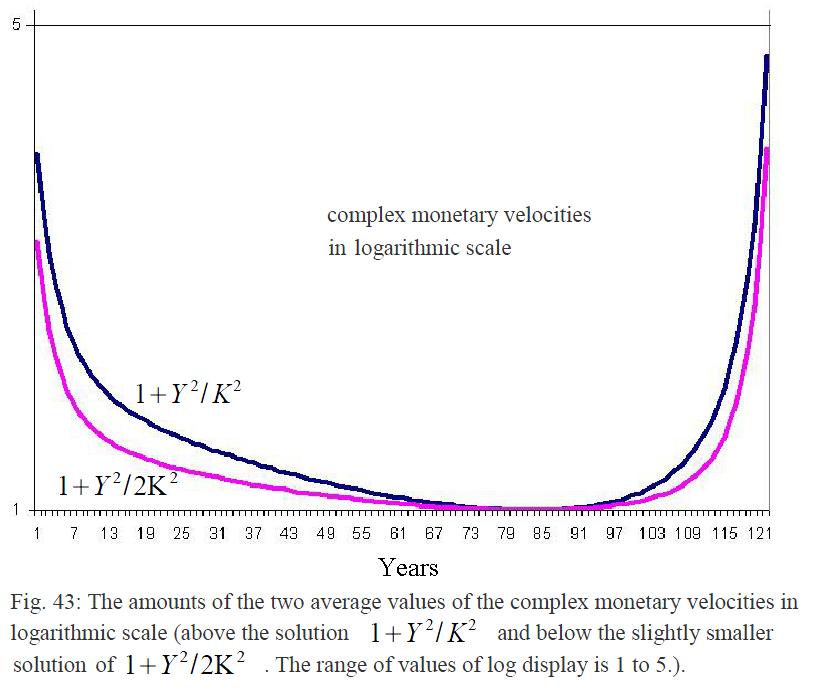
In the GMF, it proves useful, the correlation of Y with K in the complex plane to investigate. It is the complex vector

    (45.9)

the object of investigation. It now runs the imaginary axis in the Y(K)-diagram along the vertical axis and the real part along the horizontal x-axis. On the course of the real and imaginary part of the solution, we can already derive some properties for the average monetary velocity: Thus we see the course of the imaginary part corresponding to the real economy component, the typical U-shaped curve of the average velocity. Unlike the real part that corresponds to the proportion of the capital stock, where the velocity decreases and eventually becomes negative even.

 

 

Correspond to the empirical facts that could be observed as in the recent crisis that the banks due to lack of returns, no longer trusted each other. And therefore, funds withheld, instead of selling loans. The real economy on the other hand is stagnating first, but only then to re-tighten. Which can be explained by the fact that first the general economic situation warns the money to be restraint, but at the end of the growing crisis money will be exchanged increasingly into real values.

While the different development of the two contributionsandis clear, but in the real economy, however, the sum of share is the load-bearing component. The two solutions differ in little: