18 Analysis of the Basic Equations
The simplified basic system
![]() (18.1 a)
(18.1 a)
and![]() (18.1 b)
(18.1 b)
allows at hand of the structure already
some analytical statements. We consider the following a closed economy, i.e. the
foreign terms ![]() are zero or close
to zero. So obviously, GDP growth stops if
are zero or close
to zero. So obviously, GDP growth stops if![]() and
capital growth at
and
capital growth at ![]() . Further
on, GDP growth stops when at least one of the three right hand side factors is
zero:
. Further
on, GDP growth stops when at least one of the three right hand side factors is
zero:
![]() or
or ![]() or
or
![]() (18.2).
(18.2).
The case K=0 is trivial, the case![]() , however,
surprising at first glance. It means that the flow of credit dries up, if the
return on investment is zero. From the last factor, we can now estimate the
time
, however,
surprising at first glance. It means that the flow of credit dries up, if the
return on investment is zero. From the last factor, we can now estimate the
time![]() , when the GDP
growth stops non trivially:
, when the GDP
growth stops non trivially:
![]() (18.3).
(18.3).
With the realistic choise![]() this results in
this results in![]() years. After this
time GDP in the medium term falls ever further. An effect which now shows up in
developed economies like the U.S.
or the EU as well. It can be mitigated, however, due to the effect of
population growth since then the additive term
years. After this
time GDP in the medium term falls ever further. An effect which now shows up in
developed economies like the U.S.
or the EU as well. It can be mitigated, however, due to the effect of
population growth since then the additive term![]() can
feed continuing growth:
can
feed continuing growth:
![]() (18.1 c)
(18.1 c)
and from that rules:
![]() (18.4 a).
(18.4 a).
On the capital side, it looks a little better. There does the savings rate obviously the same task as population growth in GDP:
![]() (18.4 b)
(18.4 b)
In the following short analysis, we will
distinguish between direct capital driven growth (cdg)
and the indirect growth (idg) that is driven from the
coefficient of population growth![]() and the savings
rate
and the savings
rate![]() . Let us now
consider the three factors on the right hand side more precisely. The nominal
interest rate
. Let us now
consider the three factors on the right hand side more precisely. The nominal
interest rate![]() is generally a with time decreasing positive factor, but the value of
total capital coefficient
is generally a with time decreasing positive factor, but the value of
total capital coefficient![]() however continues
to rise roughly linearly with time.
however continues
to rise roughly linearly with time.
It remains the key factor![]() , which lies between -1 and 1 and is negative until
, which lies between -1 and 1 and is negative until![]() , after then it
gets positive. So we can write abbreviated, where
, after then it
gets positive. So we can write abbreviated, where![]() is a number between 0 and 1 :
is a number between 0 and 1 :
![]() and
and ![]() (18.4 c)
(18.4 c)
The importance of these two equations is that when they rule, indirect growth stops. If one wants to achieve indirect growth, it must apply the reverse:
![]()
![]() for idg-GDP
growth
for idg-GDP
growth
![]() for idg-Capital
growth
for idg-Capital
growth
![]()
![]() for idg-GDP
growth
for idg-GDP
growth
![]() for idg-Capital
growth
for idg-Capital
growth
![]()
![]() for idg-GDP
growth
for idg-GDP
growth
![]() for idg-Capital
growth
for idg-Capital
growth
(18.4 d)
Let us now consider the situations of different
time lines. The situation for![]() is relatively
trivial, as a further GDP growth is possible by a positive population growth
and/or a positive savings rate. For the period before the turning point
is relatively
trivial, as a further GDP growth is possible by a positive population growth
and/or a positive savings rate. For the period before the turning point![]() the capital
coefficient
the capital
coefficient![]() has values
between about 1/3 and 3, while the nominal interest rates slowly
fall from initially more than 10% against almost 0 at the end of
the period. So we divide in the two time periods prior to and after reaching a
coefficient of capital
has values
between about 1/3 and 3, while the nominal interest rates slowly
fall from initially more than 10% against almost 0 at the end of
the period. So we divide in the two time periods prior to and after reaching a
coefficient of capital![]() . This was
achieved in the FRG in 1967. If we now insert typical values for the
coefficients for the three phases, then the following rough estimates hold:
. This was
achieved in the FRG in 1967. If we now insert typical values for the
coefficients for the three phases, then the following rough estimates hold:
![]() ”Economic
miracle”-years36
”Economic
miracle”-years36
![]() % for idg-growth
% for idg-growth
or more generally![]() (18.5 a)
(18.5 a)
![]() normal growth years
normal growth years
![]() % for idg-growth
% for idg-growth
or more generally ![]() (18.5 b)
(18.5 b)
![]() years of crisis
years of crisis
![]() % for idg-growth
% for idg-growth
or more generally ![]() (18.5 c)
(18.5 c)
Population growth is a phenomenon that can be
controlled very badly through policy measures. As one can see a stable
population was important in the beginning, and the actually slightly declining
population of the German could never hurt much GDP growth. After the onset of
the crisis years, however, only a significant population growth could avoid
decline in the GDP in the medium-term. However, the savings rate![]() is quite
suggestible. Thus we see that in the so-called “economic miracle
years”, the savings rate had to be possibly positive37 to allow for growth. In the later
years of growth, also a slightly negative savings rate can afford growth. Since
the years of crisis a positive savings rate then is even required to allow the
indirect growth of capital to continue. Finally, we take a look at the complete
system of equations:
is quite
suggestible. Thus we see that in the so-called “economic miracle
years”, the savings rate had to be possibly positive37 to allow for growth. In the later
years of growth, also a slightly negative savings rate can afford growth. Since
the years of crisis a positive savings rate then is even required to allow the
indirect growth of capital to continue. Finally, we take a look at the complete
system of equations:
![]() (18.1 d)
(18.1 d)
![]() (18.1 e)
(18.1 e)
The foreign contributions![]() and
and![]() can therefore be
used at any time to compensate for deficits. Because when considering the case
can therefore be
used at any time to compensate for deficits. Because when considering the case![]() , then
, then![]() takes over the
role of
takes over the
role of ![]() and
and![]() takes over the
role of
takes over the
role of![]() in the prior
consideration. Due to the complex mutual dependencies of all parameters, the
possibilities of correction in practice are unfortunately not so simple.
in the prior
consideration. Due to the complex mutual dependencies of all parameters, the
possibilities of correction in practice are unfortunately not so simple.
After this introductory treatment of the structure of our system of
differential equations, we now come to the necessary integration. With
numerical38methods this is not a significant
problem, however, there will be lost inevitably important analytical
relationships. This can be avoided by the analytic integration. Analytical
solutions are so important because they only allow universally valid
quantitative results. The analytical integration even easier systems of
differential equations are often not trivial. Already our simplified model
(18.1) is not integrable in closed form. In the
alternative, but can be integrated piecewise to gain an impression of the
analytical behavior of the functions. Thus we may
regard![]() as piecewise
constant, where the integration runs only over a limited number of years.
as piecewise
constant, where the integration runs only over a limited number of years.
As a powerful tool to scientists today are good software packages for the manipulation of algebraic equations avaiable. Such programs39 can save days on computing to try the "crack" of the integrals. It shows out that, depending on whether the expression generated
![]() (18.6)
(18.6)
is positive, negative or zero, different solutions must be discussed within their respective local scope:
![]()
![]()
(![]() negative) (18.7 a and b)
negative) (18.7 a and b)
![]()
![]()
(![]() null) (18.8 a and b)
null) (18.8 a and b)
![]()
![]()
(![]() positive) (18.9 a and b)
positive) (18.9 a and b)
The![]() function
has the dimension of a frequency and is crucial for the kind of growth. The
growth rate
function
has the dimension of a frequency and is crucial for the kind of growth. The
growth rate![]() is zero for
is zero for![]() or
or![]() . Therefore, we
need to make at this point a further case distinction:
. Therefore, we
need to make at this point a further case distinction:
![]()
![]()
For ![]() (18.10 a and b)
(18.10 a and b)
or
![]()
![]()
For ![]() (18.11 a and b)
(18.11 a and b)
This can be written with the specific growth factors
![]() and
and ![]() (18.12 a and b)
(18.12 a and b)
in the following specific forms
![]()
![]() for
for ![]() (18.13 a and b)
(18.13 a and b)
or
![]()
and
![]() for
for ![]() (18.14 a and b).
(18.14 a and b).
The area around![]() is the upper
turning point of the GDP development. At beginning of the national economy, the
"good times",
is the upper
turning point of the GDP development. At beginning of the national economy, the
"good times",![]() is negative, and after the reversal point it runs into the positive
range (“bad times” of crisis). The
results are:
is negative, and after the reversal point it runs into the positive
range (“bad times” of crisis). The
results are:

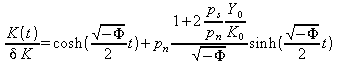
(![]() negative) (18.15 a and b)
negative) (18.15 a and b)
and

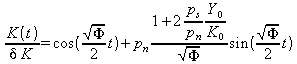
(![]() positive) (18.16 a and b)
positive) (18.16 a and b)
For clarity, one can now finally write
![]() and
and ![]() (18.17)
(18.17)
with the specific growth forms![]() :
:
![]()
![]()
(![]() negative (D1) ) (18.18 a and b)
negative (D1) ) (18.18 a and b)
and
![]()
![]()
(![]() positive (D2) ) (18.19 a and b)
positive (D2) ) (18.19 a and b)
and as usual
![]() or
or ![]()
![]() or
or ![]()
(![]() Null (D3) ) (18.20 a and b)
Null (D3) ) (18.20 a and b)
for ![]() or
or
![]() with the simple
abbreviations
with the simple
abbreviations
![]() and
and
![]() and
and
![]() (18.21)
(18.21)
for clarity.