40 Field Equations of Economics

We now will derive the main field equations of economics.

The units 1/y and cur./Buy in standard quantity equation disagree, which should not happen for the variational calculus as units [.] have to be. Thus we try to define them in better useable⁸¹ quantities for variational calculus. Instead of the usual dimension of money [currency] we use the more meaningful money dimension of „purchasing power“ in dimension of buy/cur . The inverse dimension then is the “value of goods” in dimension of cur/buy. Thus for the use of Lagrangians in economy we define VoG:=”Value of Goods” and VoM:=”Value of Money” with VoM = 1/ VoG which leads to:

  or   

and by definition:

    (40.1)

Thus we get:

or   with    and     and like we started in this chapter we get the matrices:

or

    (40.2)

which leads like before to:

    (40.3)

which seems to be:

Now we invest again Euler-Lagrange, but now with corrected values:

   and        (40.4)

which leads to

   with  

(40.5)

which results in

  gives 

  gives   

  gives 

The last equation is equal to    or     and so we get:

  gives 

  gives   

  gives   

Addition/subtractions/multiplication like before of the main equation now gives:

  plus   

results in        (40.6)

  minus  

results in         (40.7)

  plus   

results in         (40.8)

  minus   

results in         (40.9)

The products of the results then gives

   and        (40.10)

which results by division of the two equations in

    (40.11)

This nonlinear differential equation

    (40.12)

is the Basic Differential Quantity Equation (BDQE) of Economics with Lagrangian applied. We call it basic, as it splits up in just the two main components R and I. Of course it can be split up to any number of components as one needs, but splitting up at least into the two main parts is essential for deeper analysis. The BDQE is rather complicated to solve as it is strictly nonlinear and thus will be delayed to further science in a later issue of this book. But even without explicit solving, which needs some more definition of formulas, the BDQE can be investigated some further.

Next we have to show, that the BDQE is identical to the common known classical quantity equation MV=HP in the linear quasi-constant case . For this we have to assume, that the banks own business I does play no big role of influence to the GDP, and thus all I-values can be set to be zero. Thus we get just one component left:, from which we now just can take the root which gives . Written in little other notation we will call this the Simplified Linear Differential Quantity Equation (SLDQE) of Economics:

    (40.13)

If the values M, P are assumed to be quasi-constants, as can be assumed for small differences in time always approximately (which is done regularly in classical economy), one can multiply the equation by the needless dt. And thus one gets of course the classical expression of the classical simplified linear Quantity Equation (csl-QE) by just choosing the meaningful positive solution to

The simplified quantity equations are useful, if one needs no deep insights and/or no large time scale of investigation. The classical QE gives, as commonly known, just approximate (locally) valid results. But then we have to use the differential form of it, as we then have to investigate the evolution of the functions in time. And so we may define the altered classical equation

    (40.14)

We have used the simeq-sign instead of an equal sign for the linear approximation, which is just to demonstrate the approximate state of any of this linear equations. This is also due to the, in physics well known fact, that every interdependency between two forces always leads in principle to nonlinear differential equation.

Now we derive the Field-Equations:

As systems of linearized differential equations are much easier to solve, the question thus is, when may I linearize the strictly nonlinear differential equation and how far can I go with it? As we could show in the first part of the book, the linear case is given for all times until deep crisis occurs, but after that it can be indeed questioned. For this reason, we start further investigations with the nonlinear BDQE, from which we will get some more insights into the main economic behaviour. The DQE

may be written more simpler with the use of complex vectors. Such complex numbers have the usual euclidic metric defined by using definition of the conjugated complex with. But instead of the usual euclidic norm we define now a special p-norm for the k-dimensional pseudo-complex vector:

    (40.15) .

This pseudo-complex number is best represented by using a socalled pseudo-riemanian metric represented here by the Minkowsy-tensor

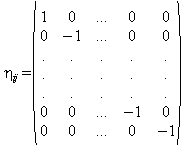    (40.16)

which thus gives the rule for the length of our pseudo-complex vector

  of any dimension     (40.17)

with norm

    (40.18)

So we can now redefine our two-dimensional basic vectors to

.

With       (40.19).

From this follows directly by applying the squareroot and we finally get

    (40.20)

the much simpler looking Pseudo-Complex Differential Quantity Equation (PCDQE). From this arrangement we can see the fundamentals of economics now more clearly. As we have four vectors of the same principal form, we see that both sides of the equation builds up its own footage area. This can be seen by the fact, that the scalar product of a vector is given by

= spanned footage

of the two vectors. Thus the effect of QE is the fact, that the area spanned by the money supplyand the area spanned by merchandisehas to be equal over time:

    (40.21)

which can be thus also written as

    (40.22)

whereis the angle between the R- and I-components on the money side, andthe angle between the R- and I-components on the merchandise side.

 

As the vectorsmay have any dimension, we can say that (40.22) is the

Fundamental Geometric Law of Standard Substitutional Economics.

 

For example, to incorporate wages (W) and the accompanied labor (L) into the equation, this can be done by splitting the money supply to the real economyinto the supply for buying goods (G) and buying labor (wages: W). Thus we just may define the vectors

;;

;

as our now 3-dimensional system, where instead of equal areas now equal cubes are to be served. This system of splittings can be done to any desired precision, and thus complexity and dimensionality. By some new greek-symbols for our definition of the p-norm pseudo-complex vectors of any dimension the general nonlinear QE is written as:

    (40.23)

Or taking the root, one gets two possible solutions, which have in principle both to be checked for usability:

    (40.24)

Hereandare pseudo-complex matrices with matrix-summation norm, vector normand the sub-indexdenotes the time-derivative respectively. The in the last equation used Index-notation lets look the equation much like the classical QE approximation, but it is entirely of an other deeper meaning. Looking ad the subscripts we see, that the perfect symmetry is broken now, although on both sides the summation-index-sum spp,t agrees, the implications for M and H are but indeed slightly different. This symmetry-breaking between H and M is indeed the most important fact for growth and crisis as well.