46 Higher Orders of the Tangent

With L=0, of course, are their powers back to zero, so that higher-ordereffects with

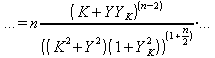
    (46.1)

 
or as

    (46.2)

 
one can write to investigate. In particular, results from the last equation the fact that, because at least one of the factors must be zero, and then the ancillary claims

    (46.3)

or     (44.4)

are justifiable. The first equation is nothing more than our original equation, the second however, can be exploited further. The latter but is not resolved afterelementary. For n=1, although there is a fairly complicated basic solution

    (46.4)

with abbreviations:

    (46.5)

which is, however, of little benefit. The interesting solutions up from n=2, on the other hand can not be solved elemental. But one can make an approximation for the inner region of the solution, as we know that'sin normal times. Thus one can justify forthe need of an approximation:

    (46.6)

which results in the two approximate solutions:

    (46.7)

Using the abbreviation of the capital coefficient asthis gives

 

    (46.8)

 
wherein the first of the higher orders is given by n=2:

    (46.9)

 Although this approximation is not very good, it clearly shows, however a similar trend as in the previously known solution of the SMF.  The difference lies in the last section, where the crisis is already in the lower phase: The mean velocity increases significantly at the end, instead of decreasing. The reason for this is that in the last phase, as already discussed, for the preservation of quantity equation a highis necessary. Whether it's the fact that one is pumping fresh money into the system, or that investors will convert more unprofitable money into real property values.

The higher orders, we can summarize for any linear combination of solutions, in analogy to the Taylor series

     (46.10)

and because

    (46.11)

results for large, a further approximation:

    (46.12)

The second factor is now adjusted for, and therefore we can isolate the total faculty. Because of the known exponential series representationthe sum total of the rest can be approximated87 to

    (46.13)

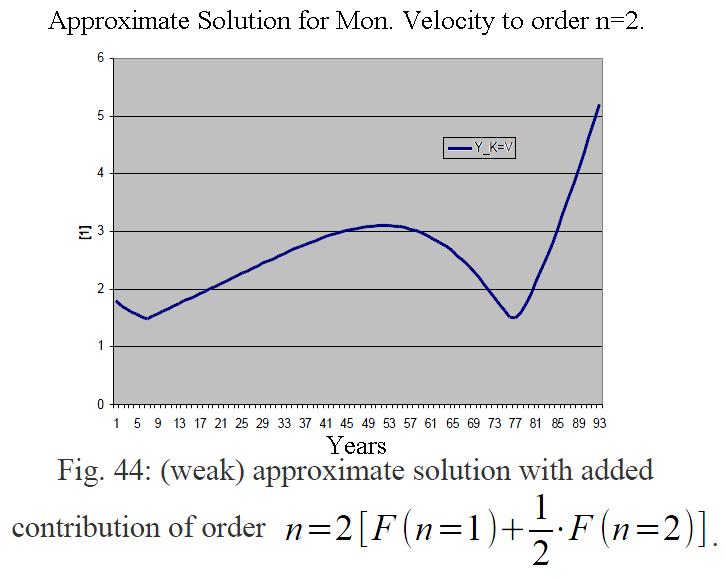
The four approximations (+, +), (-, -), (+, -), (-, +) can be used to estimate higher order effects on the average value of, wherein the (+, +) solutions results are shown in the curve below: